#ifndef DFT_H
#define DFT_H
#include <algorithm>
#include <complex>
#include <numeric>
#include <vector>
// DFT is a header-only discrete Fourier transform implementation written in
// C++14. Libraries often use optimisations that restrict dimensions of the
// sample array (power of two) but without these limitations we can explore the
// algorithm and apply it where we couldn't use a "fast" implementation. It was
// originally written to study the characteristic spectral response of my
// various musical instruments but it can be applied in other domains. The
// calculate() routine takes a pair of STL container iterators and returns the
// Fourier transform as a vector of bins. We could consider parallelising the
// matrix calculation but I've elected to keep the library simple
// (single-threaded) and delegated the multi-core utilisation to the makefile:
// the build process generates multiple images in parallel.
//
// https://en.wikipedia.org/wiki/Discrete_Fourier_transform
// https://jackschaedler.github.io/circles-sines-signals
namespace dft {
template <class T> constexpr T pi = T(3.1415926535897932385);
template <typename Iterator>
auto calculate(const Iterator begin, const Iterator end) {
// For each Fourier bin we need to iterate over each sample - O(n^2) - but we
// will return only half as many bins as samples. The upper half is a mirror
// image of the lower.
const double total_samples = std::distance(begin, end);
// This routine will return the results as a container of frequency bins.
std::vector<double> dft;
dft.reserve(total_samples / 2);
// The "twiddle matrix" is usually generated up front but as we're performing
// a one-shot calculation it can be refactored into a single loop. Normally
// you would expect to see integer array indices but here a floating-point
// counter is used to avoid a cast in the subsequent calculation.
for (double k = 0.0; k < total_samples / 2; ++k) {
// Definition of our Fourier function. Note the sample index (n) is
// incremented during the calculation.
const auto sinusoidal = [&total_samples, n = 0.0,
&k](const auto &sample) mutable {
using namespace std::complex_literals;
return exp(2i * pi<double> * k * n++ / total_samples) * double(sample);
};
// Iterate over all samples passed to this routine, calculate the response
// and store the result. See the Wikipedia link above for the details of
// the algorithm.
std::vector<std::complex<double>> fou;
std::transform(begin, end, std::back_inserter(fou), sinusoidal);
// Store the absolute sum of all responses for this frequency bin and scale
// it by the window size (number of samples).
dft.emplace_back(std::abs(std::accumulate(std::cbegin(fou), std::cend(fou),
std::complex<double>{}) /
total_samples));
}
return dft;
}
} // namespace dft
#endif
BAMBOO DRONE
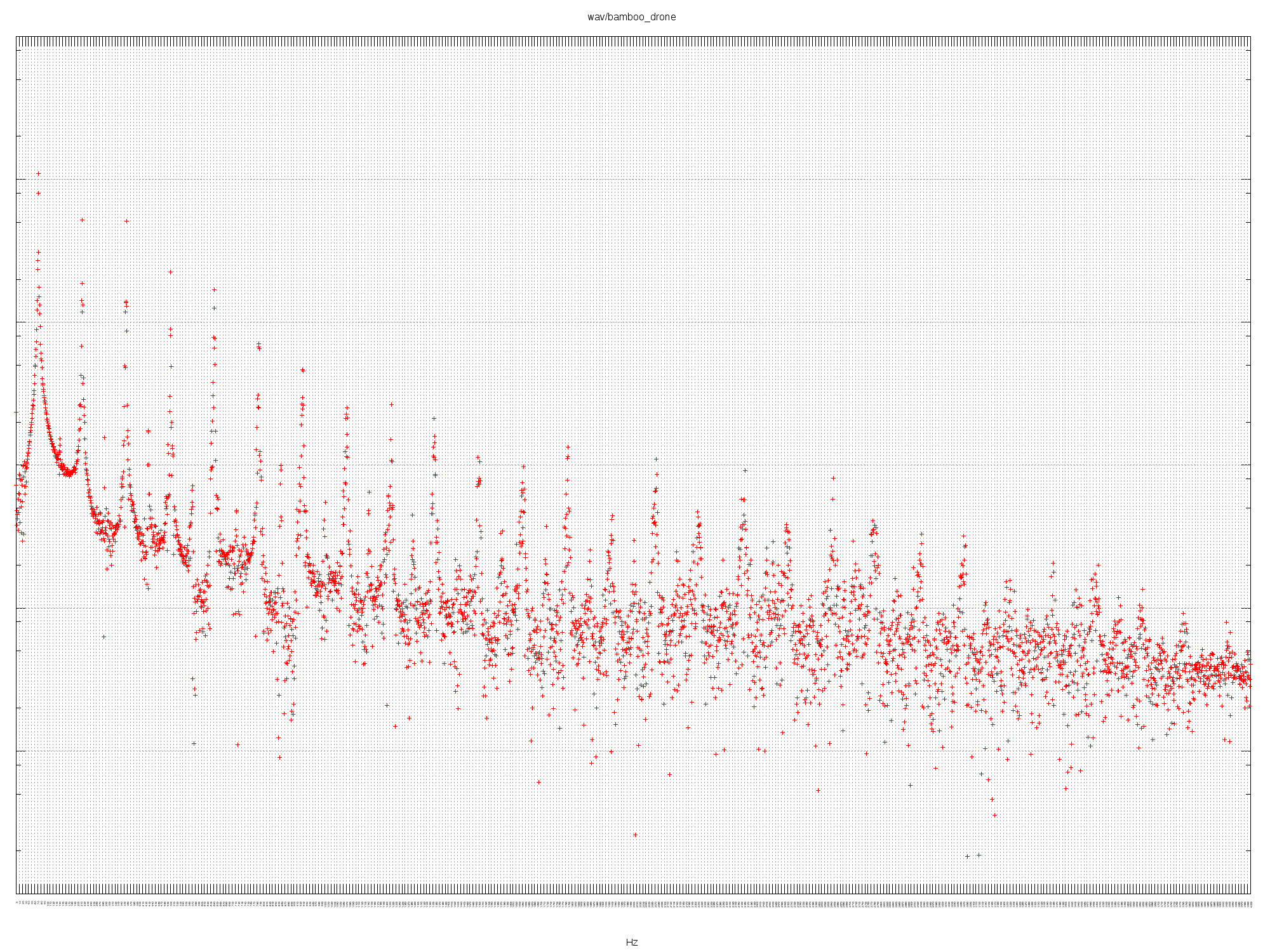 A cheap bamboo didge with a Sugru mouthpiece. Fundamental of 73 Hz (D2), with
lots of harmonics across the whole frequency range. Interestingly it’s skipping
every other overtone. An unrefined sound and quite difficult to play (poor back
pressure).
Listen to the audio.
A cheap bamboo didge with a Sugru mouthpiece. Fundamental of 73 Hz (D2), with
lots of harmonics across the whole frequency range. Interestingly it’s skipping
every other overtone. An unrefined sound and quite difficult to play (poor back
pressure).
Listen to the audio.
DIDGERIDOO BIG TONY DRONE
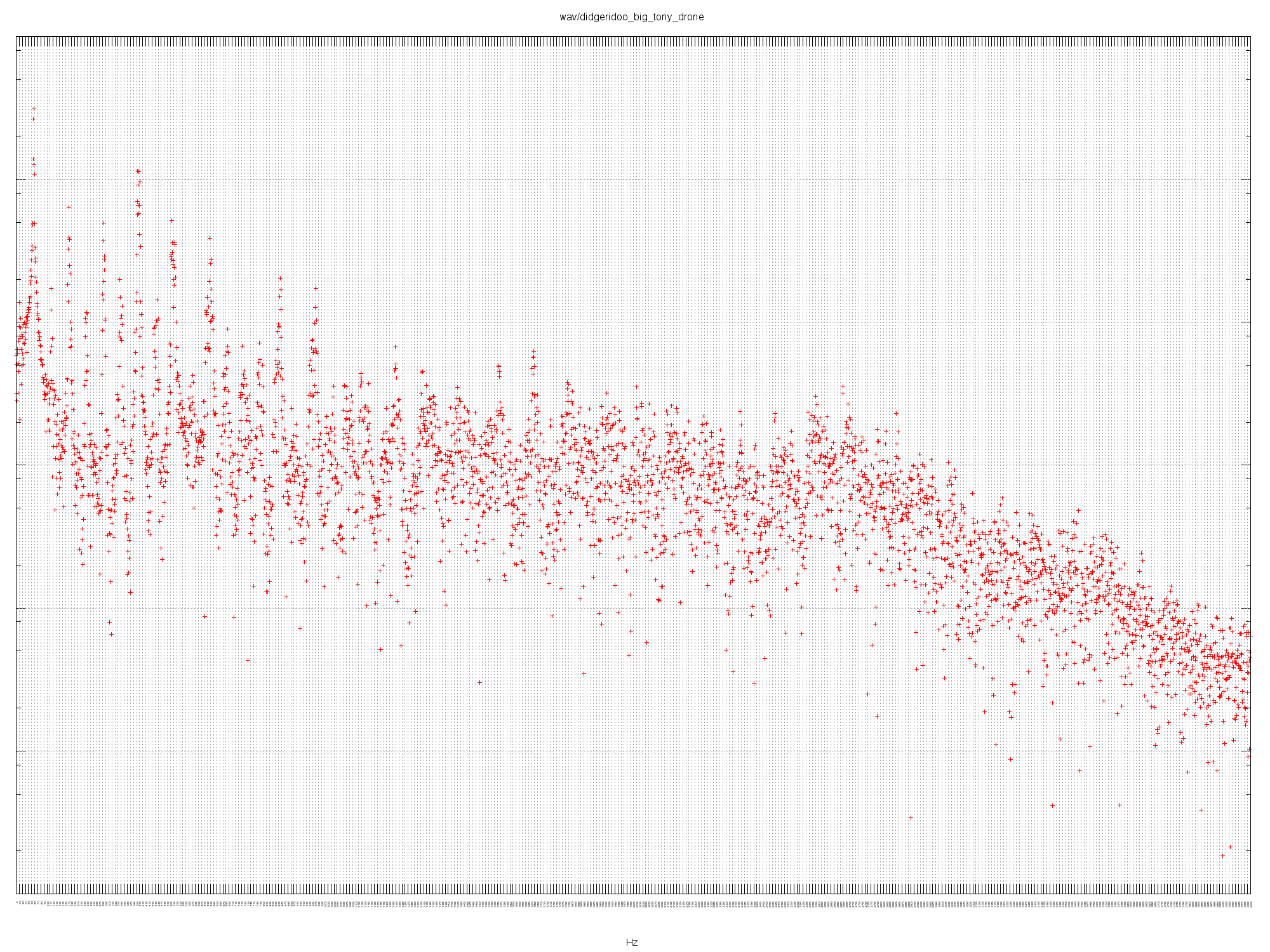 Fundamental of 58 Hz (Bb1). Key intervals are 1, 3, 5 and 7 which is Bb Major 7.
This didgeridoo was liberated from the dump and is probably Eucalyptus:
woolybutt, bloodwood and stringybark have been suggested. Very good back
pressure.
Listen to the audio.
Fundamental of 58 Hz (Bb1). Key intervals are 1, 3, 5 and 7 which is Bb Major 7.
This didgeridoo was liberated from the dump and is probably Eucalyptus:
woolybutt, bloodwood and stringybark have been suggested. Very good back
pressure.
Listen to the audio.
DIDGERIDOO BIG TONY TOOT
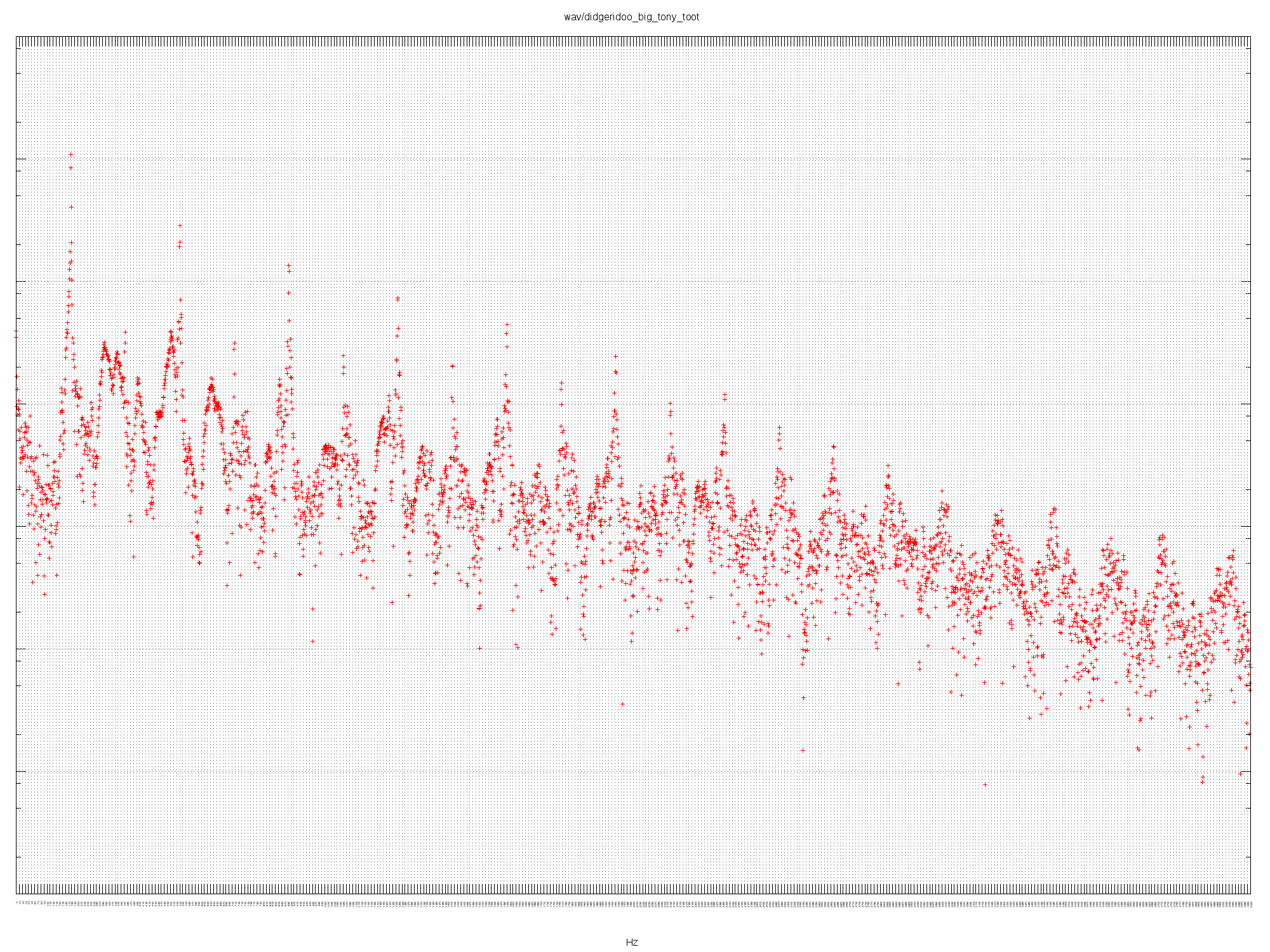 The toot has a fundamental of 178 Hz (F3) which is a fifth above the drone.
There’s also lots of activity in the higher frequencies at least up to 4 KHz.
Listen to the audio.
The toot has a fundamental of 178 Hz (F3) which is a fifth above the drone.
There’s also lots of activity in the higher frequencies at least up to 4 KHz.
Listen to the audio.
GLASS1
 Listen to the audio.
Listen to the audio.
GLASS2
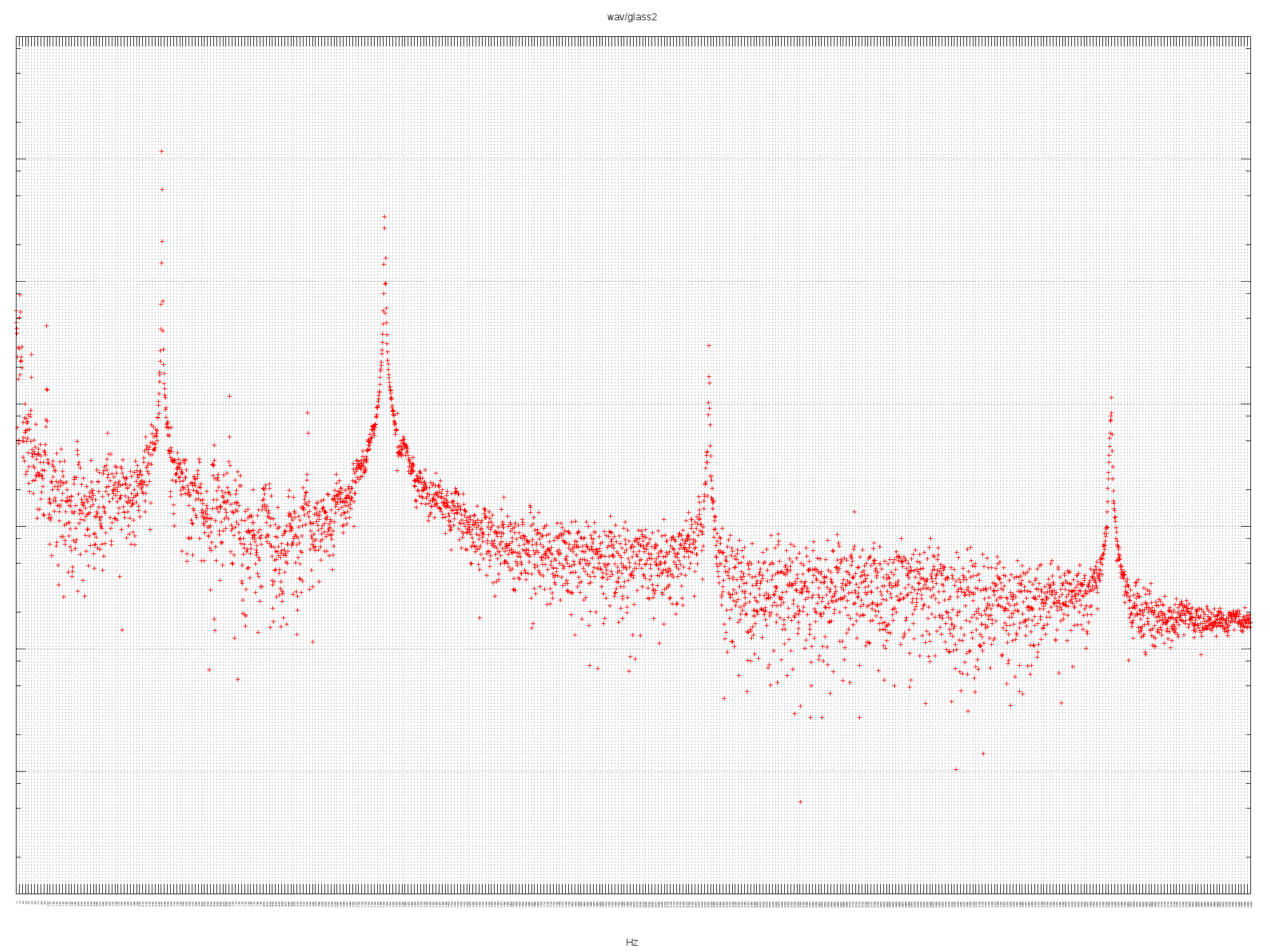 Listen to the audio.
Listen to the audio.
GLASS3
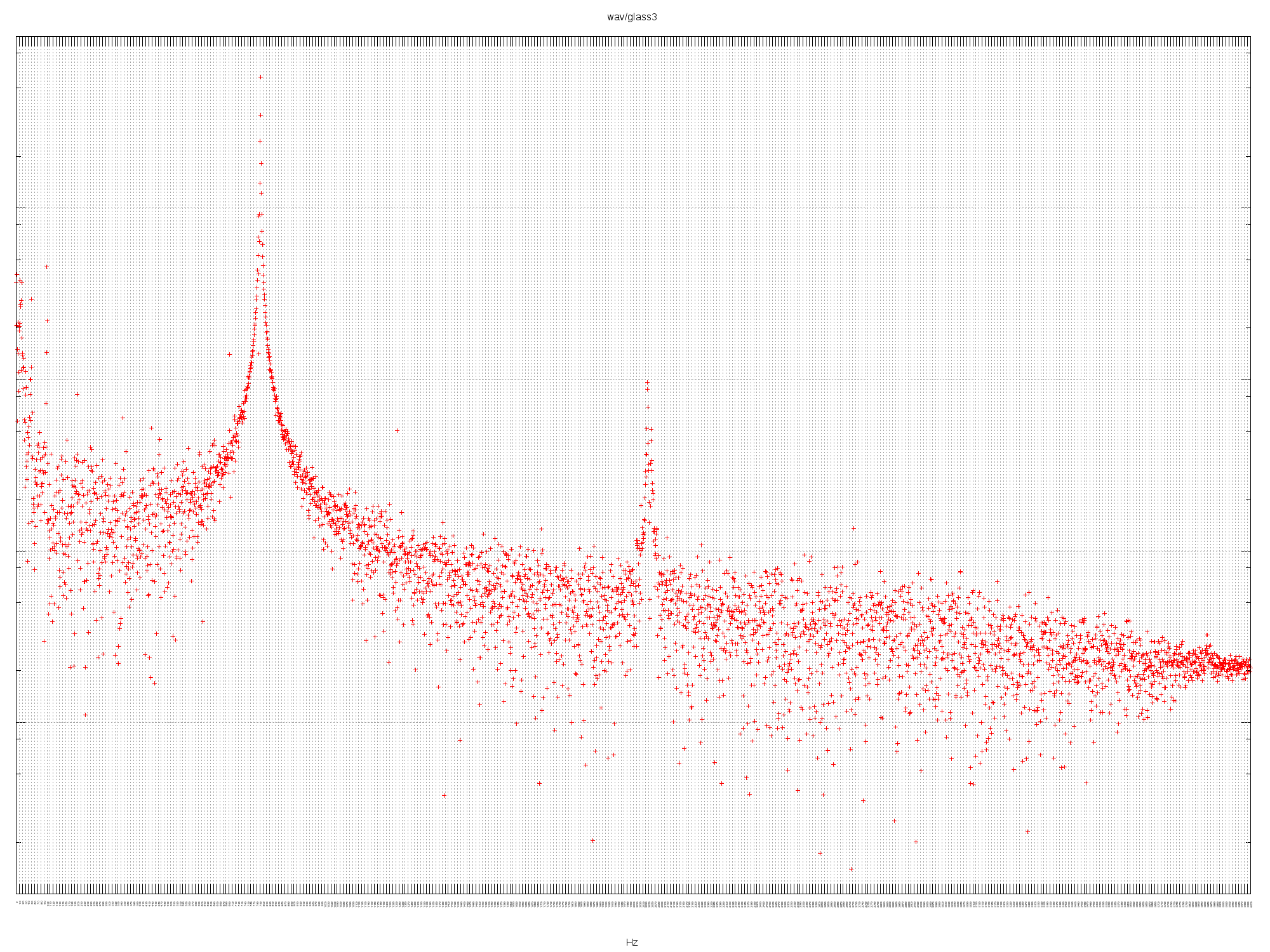 Listen to the audio.
Listen to the audio.
GLASS4
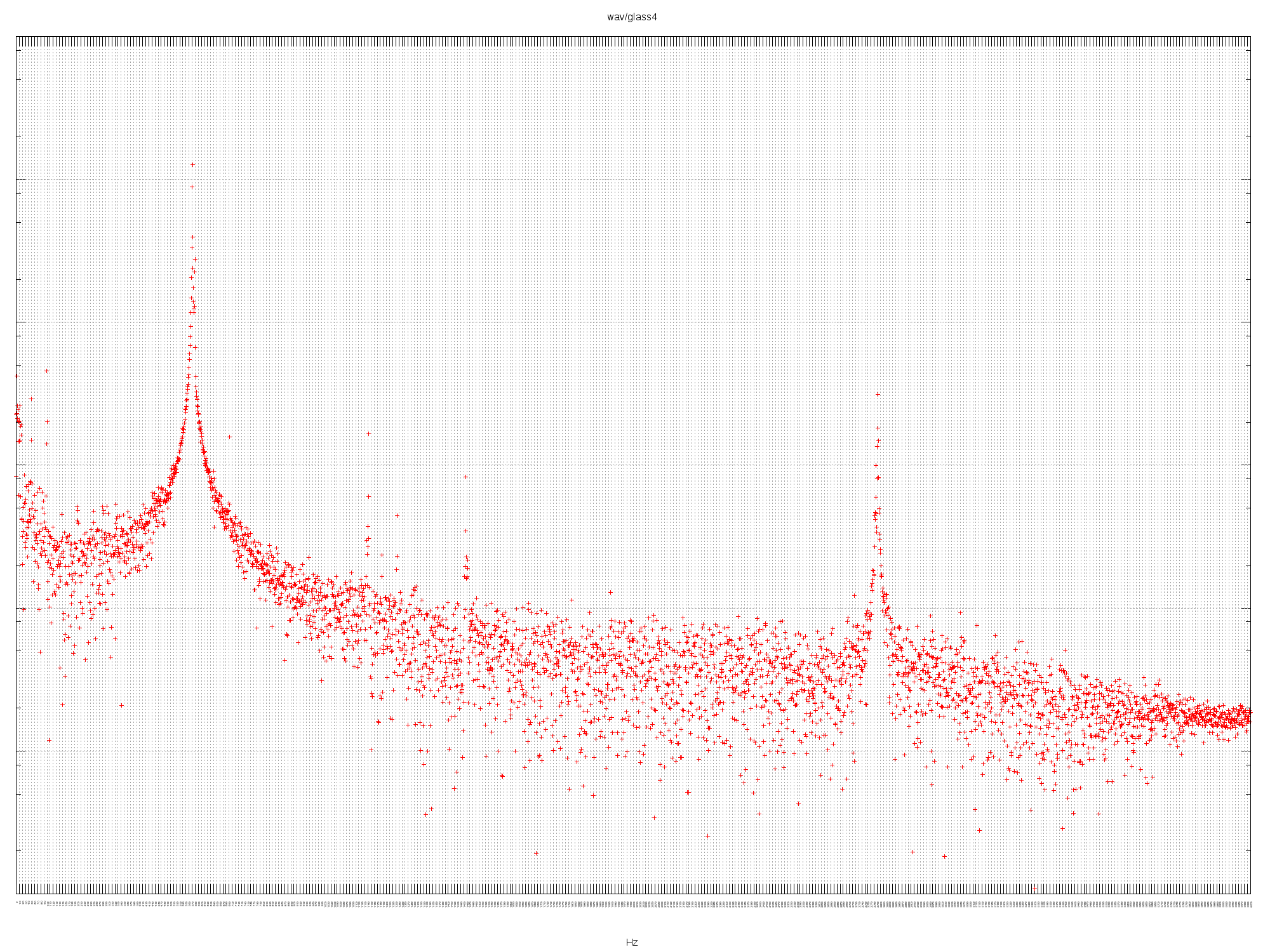 Listen to the audio.
Listen to the audio.
GLASS5
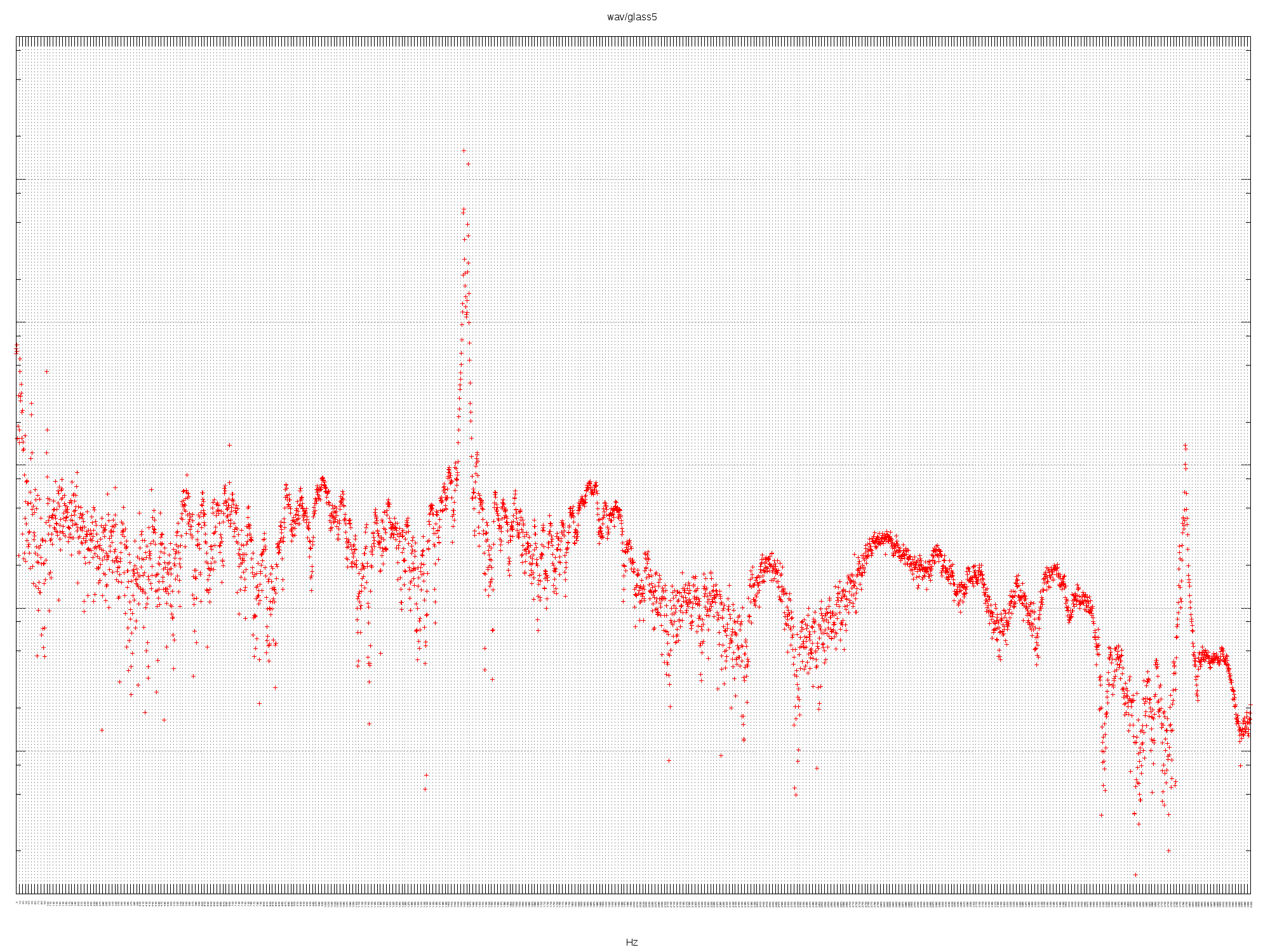 Listen to the audio.
Listen to the audio.
HOBGOBLIN DIDGE 8000
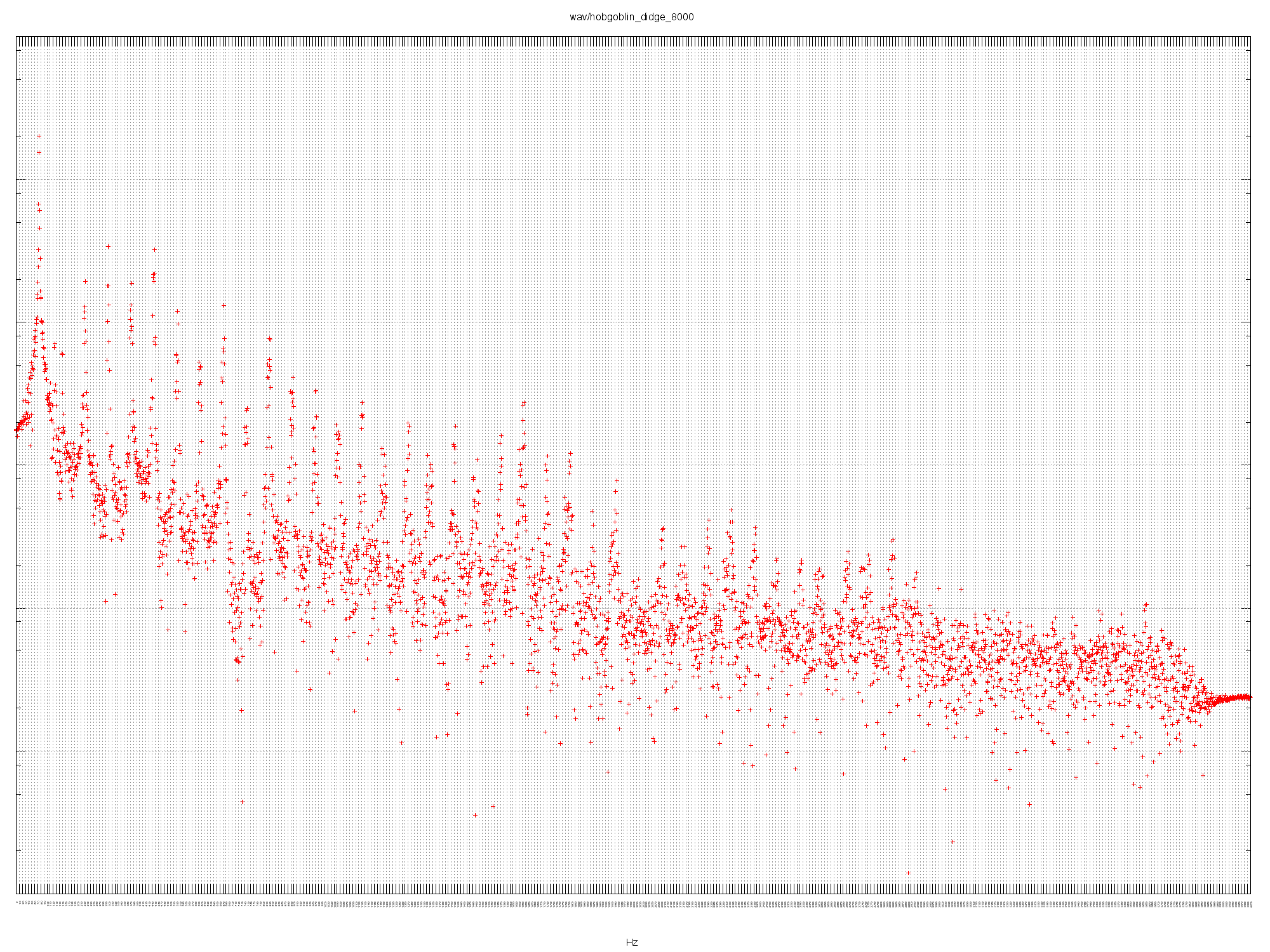 Peaks at 75, 149, 224, 299 374, 448 Hz.
Peaks at 75, 149, 224, 299 374, 448 Hz.
Fundamental of 75 Hz is somewhere between D2 and D#2. The first octave isn’t very strong but the next few overtones have equal presence. Overall it’s probably tending towards a D-Major.
73.42 D2
220.00 A3
293.66 D4
369.99 F#4
440.00 A4
Listen to the audio.
JF FIBREGLASS SLIDE
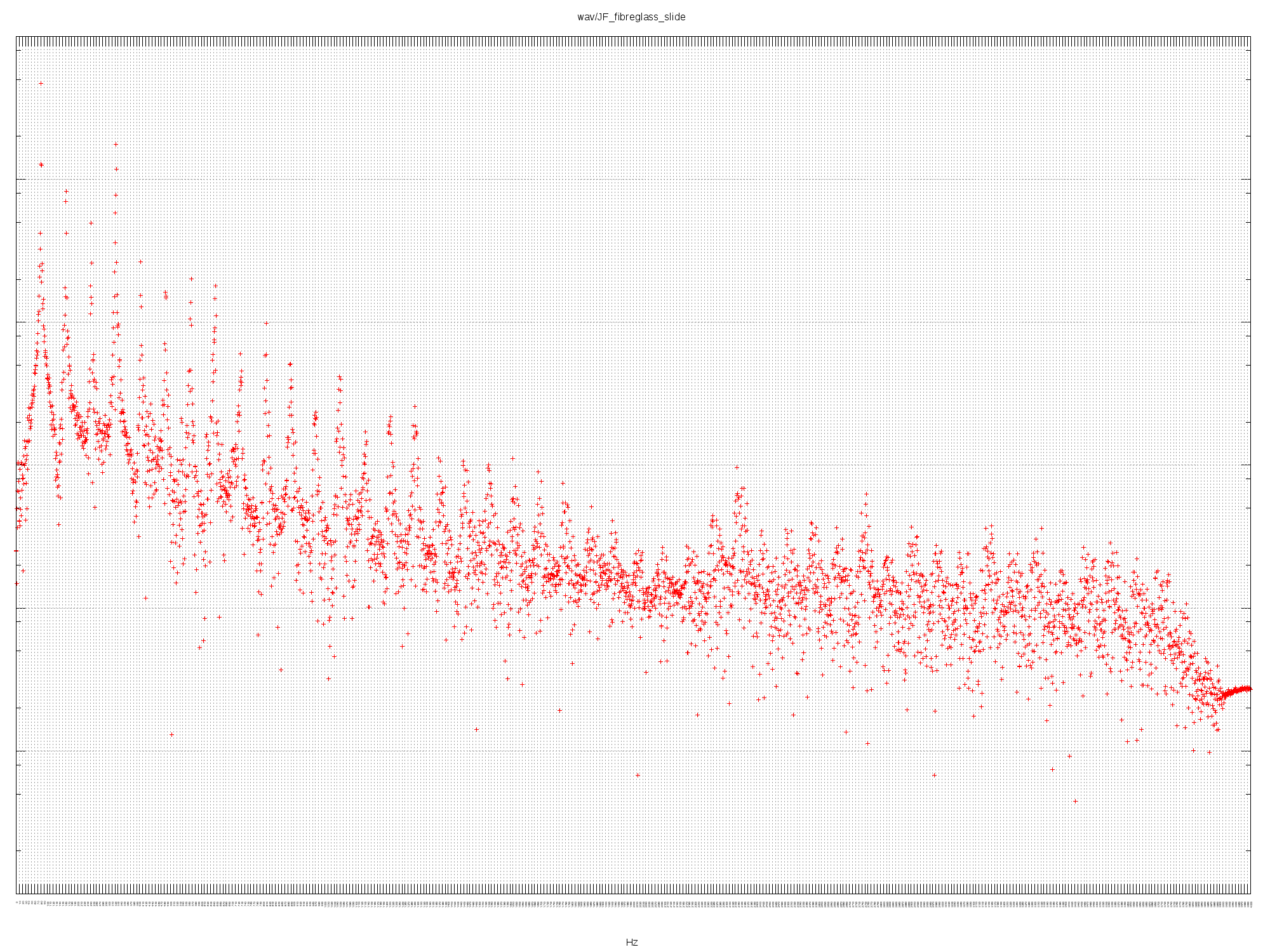 Fibreglass didge. A fundamental of 82 Hz (E2). First octave, fifth (B3) and
second octave all quite strong.
Listen to the audio.
Fibreglass didge. A fundamental of 82 Hz (E2). First octave, fifth (B3) and
second octave all quite strong.
Listen to the audio.
KP GUEST
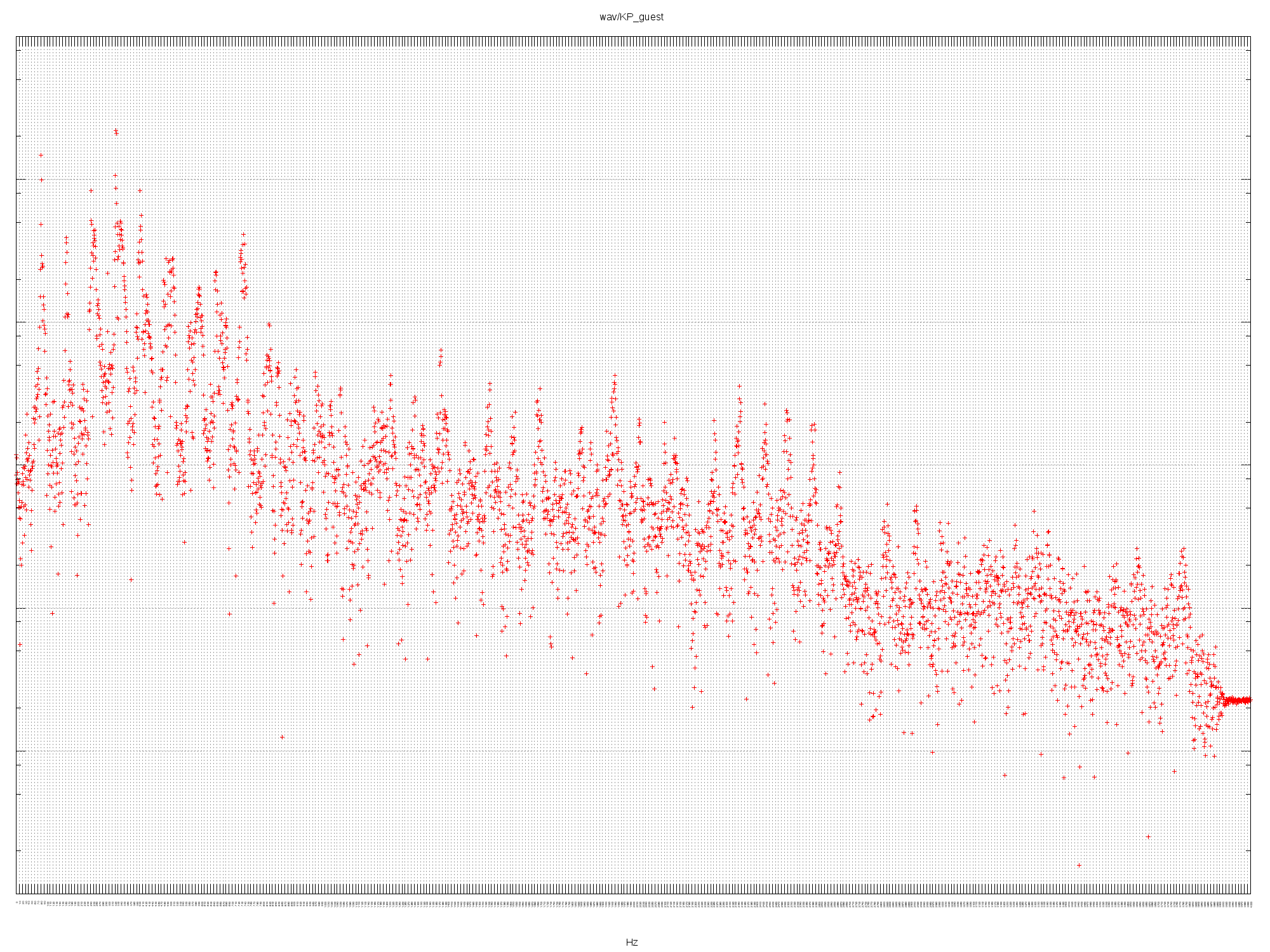 Fundamental of 83 Hz (E2) with two octaves and a fifth (B). There’s also a
hint of 403 Hz (a slightly sharp G4): a minor third. See the
scale on Wikipedia.
Listen to the audio.
Fundamental of 83 Hz (E2) with two octaves and a fifth (B). There’s also a
hint of 403 Hz (a slightly sharp G4): a minor third. See the
scale on Wikipedia.
Listen to the audio.
PIANOBB2
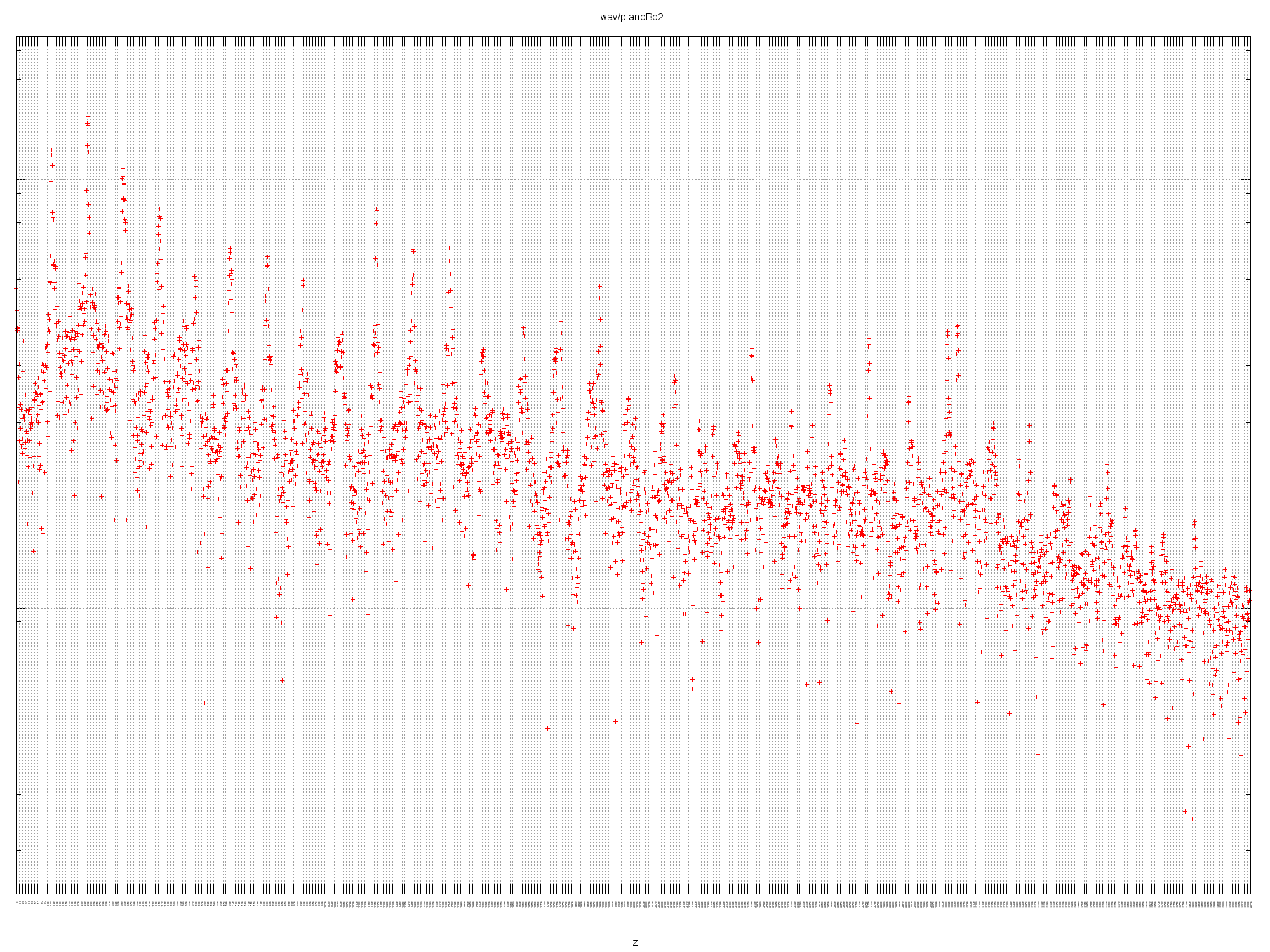 Striking the A2 key on a baby grand piano (no pedal).
Listen to the audio.
Striking the A2 key on a baby grand piano (no pedal).
Listen to the audio.
SINGING BOWL1
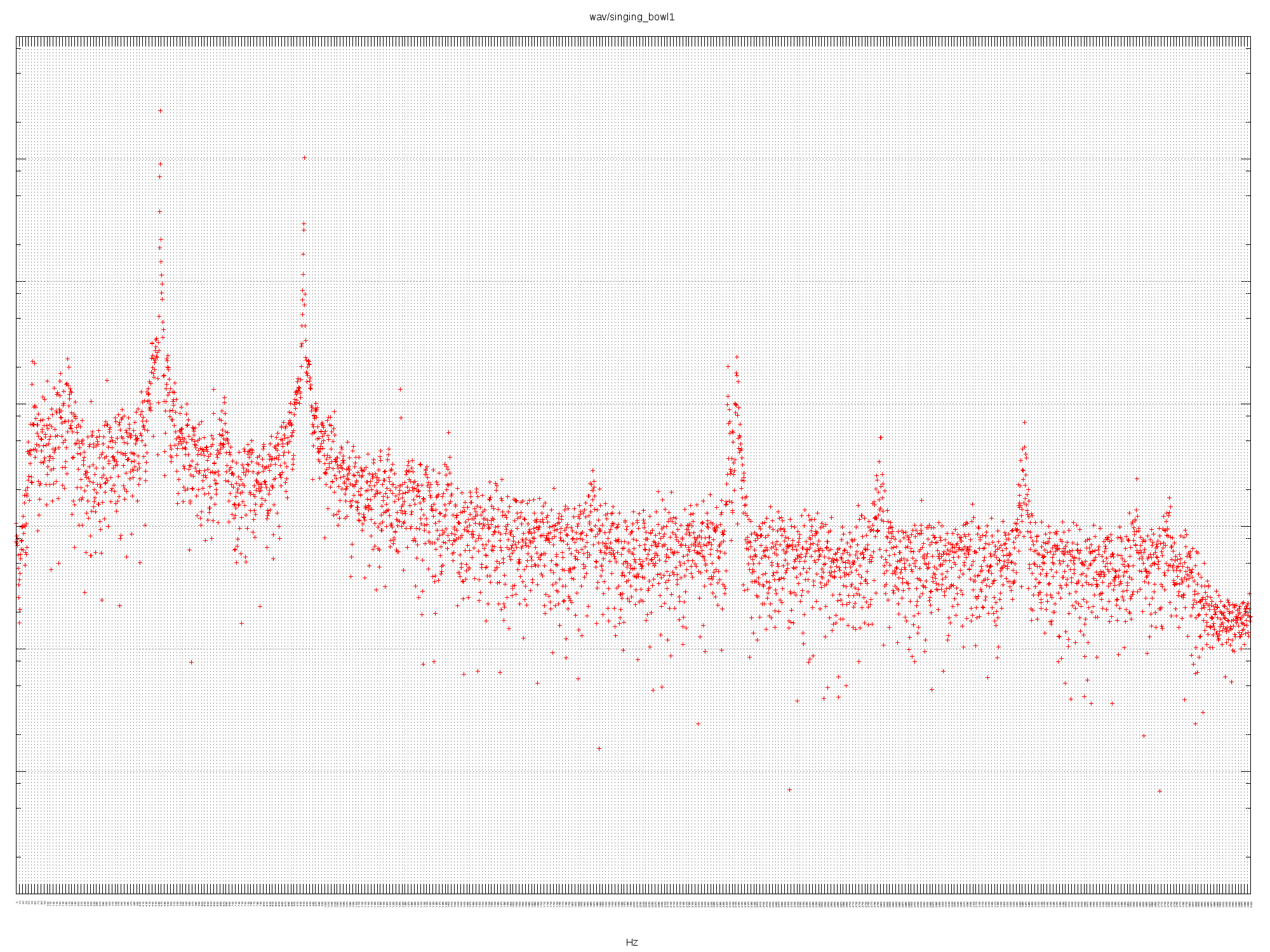 Fundamental of 469 Hz (close to A#4) and first octave of 936 Hz. The only bowl
with a pronounced octave.
Listen to the audio.
Fundamental of 469 Hz (close to A#4) and first octave of 936 Hz. The only bowl
with a pronounced octave.
Listen to the audio.
SINGING BOWL2
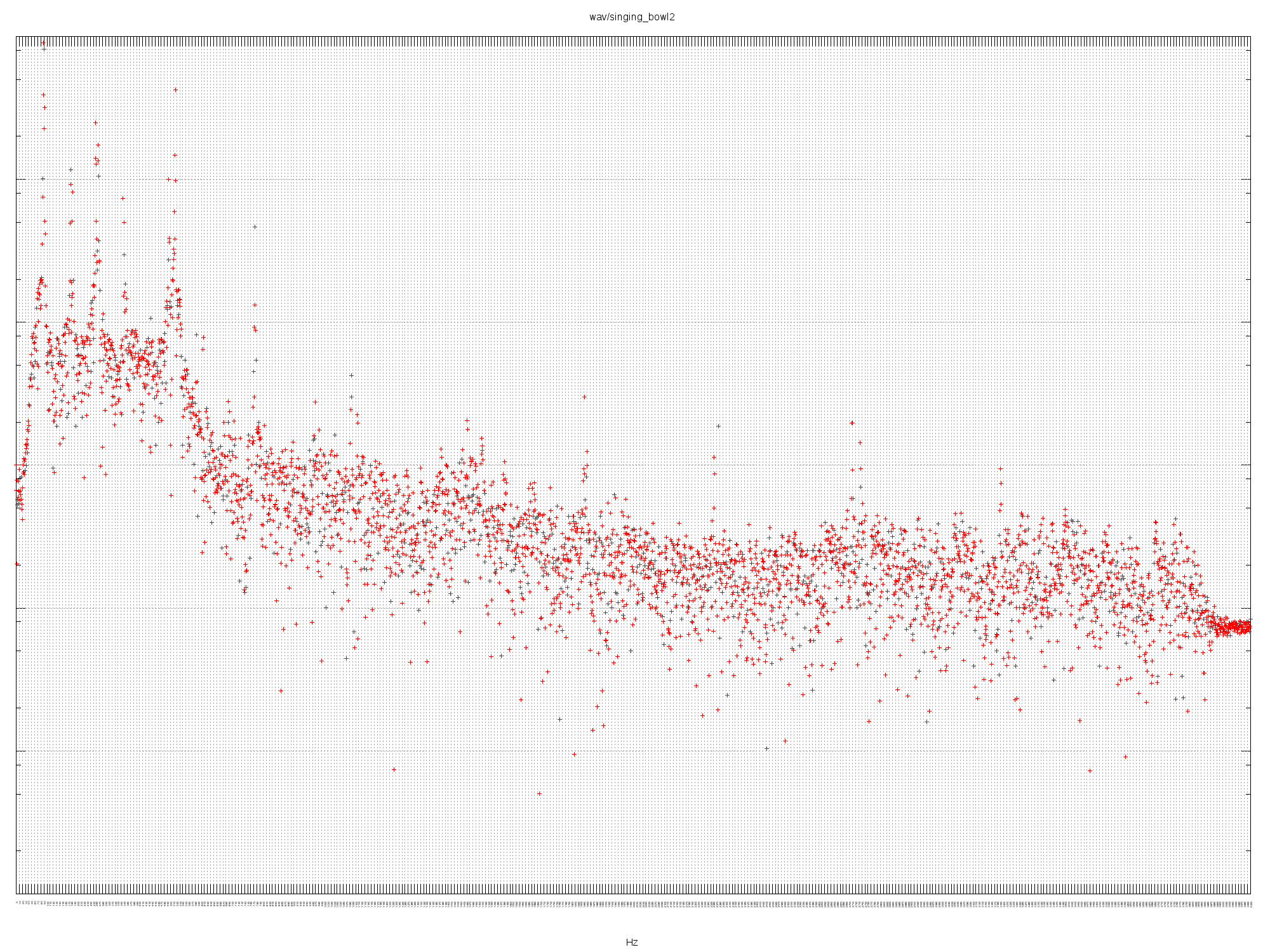 Fundamental of 90 Hz, close to F2. Significant peaks at 259 Hz and 517 Hz
(fifths). Very complex response, I suspect this is a hand-made metal bowl. (I
recorded the bowls in the dark so I’m not sure which video was which.)
Listen to the audio.
Fundamental of 90 Hz, close to F2. Significant peaks at 259 Hz and 517 Hz
(fifths). Very complex response, I suspect this is a hand-made metal bowl. (I
recorded the bowls in the dark so I’m not sure which video was which.)
Listen to the audio.
SINGING BOWL3
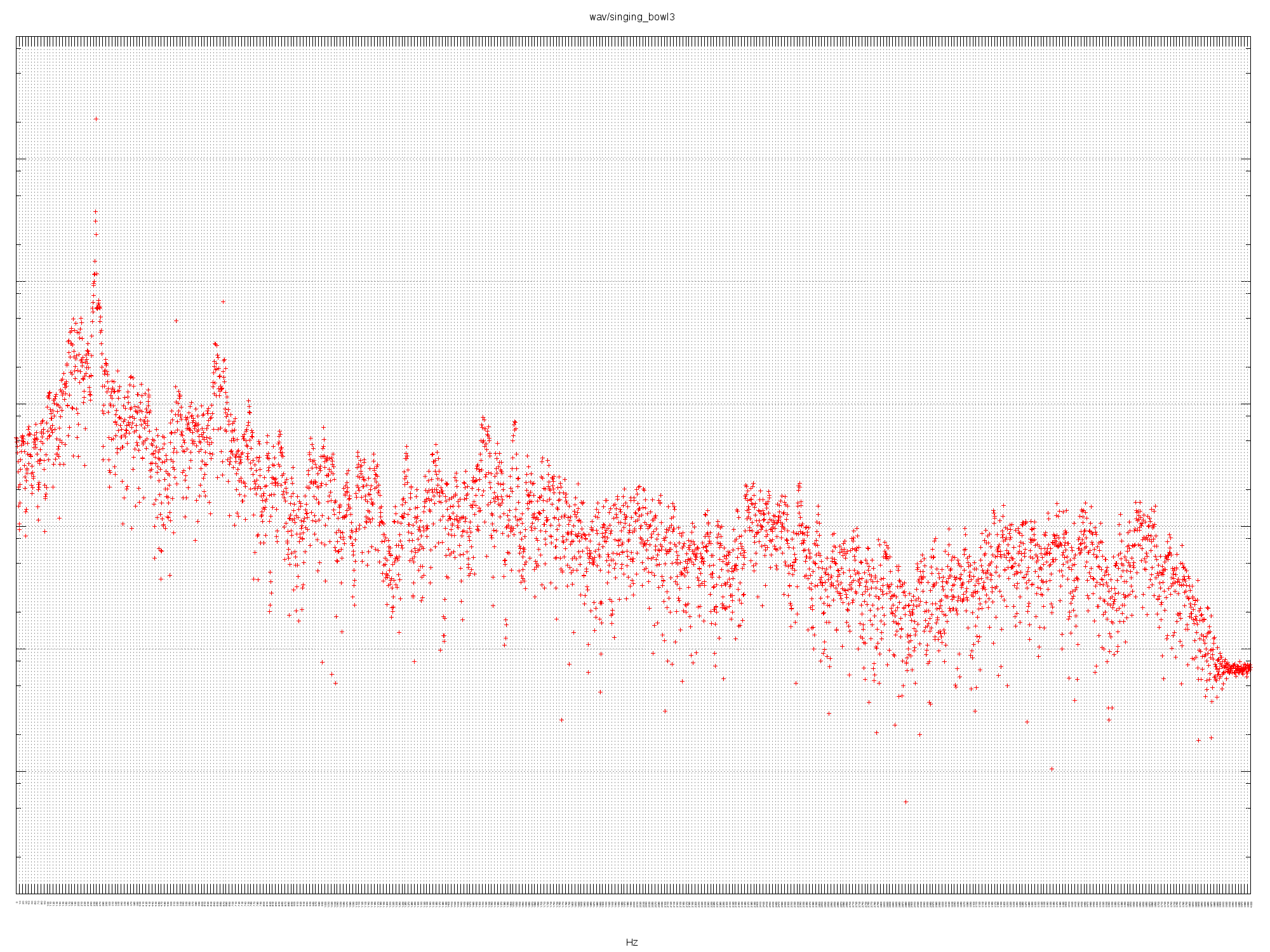 Fundamental exactly 261 Hz (C4). Maybe a touch of a fifth but really very little
overtone presence.
Listen to the audio.
Fundamental exactly 261 Hz (C4). Maybe a touch of a fifth but really very little
overtone presence.
Listen to the audio.
SINGING BOWL5
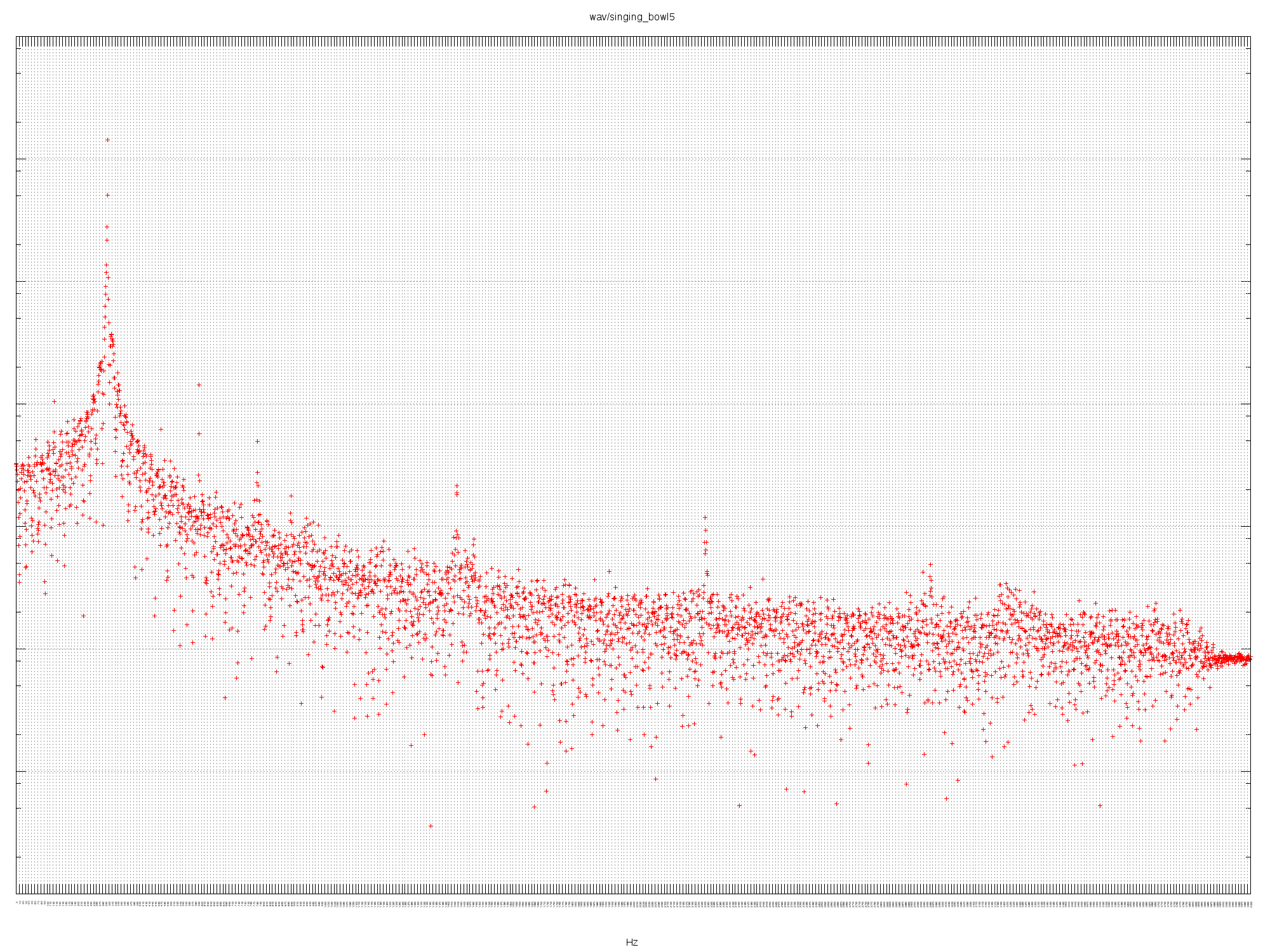 Extremely pure fundamental of 298 Hz. Halfway between D4 and D#4.
Listen to the audio.
Extremely pure fundamental of 298 Hz. Halfway between D4 and D#4.
Listen to the audio.
SYNTHESISED CHORD
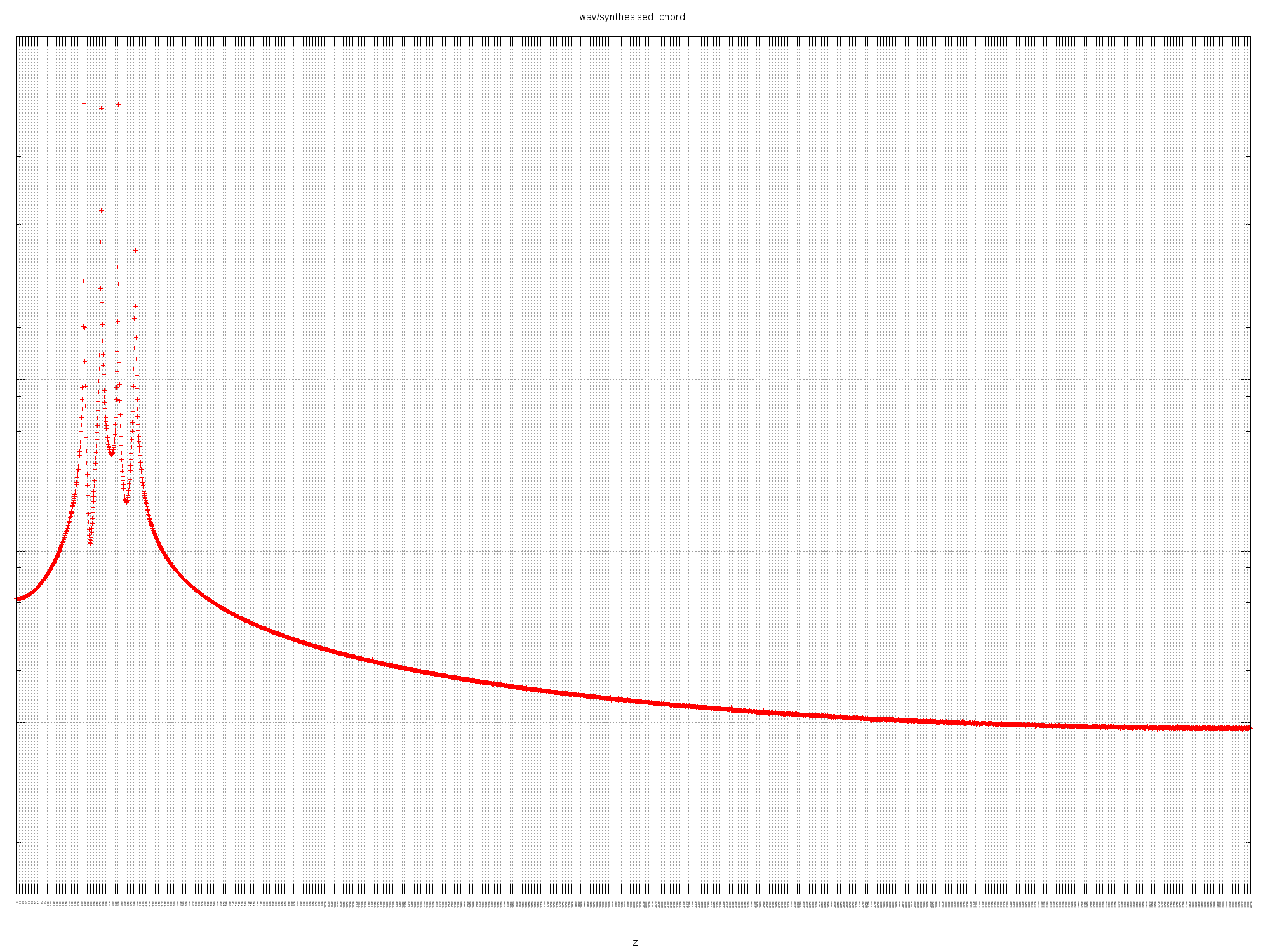 Listen to the audio.
Listen to the audio.
SYNTHESISED CHORD WHOLE FREQS
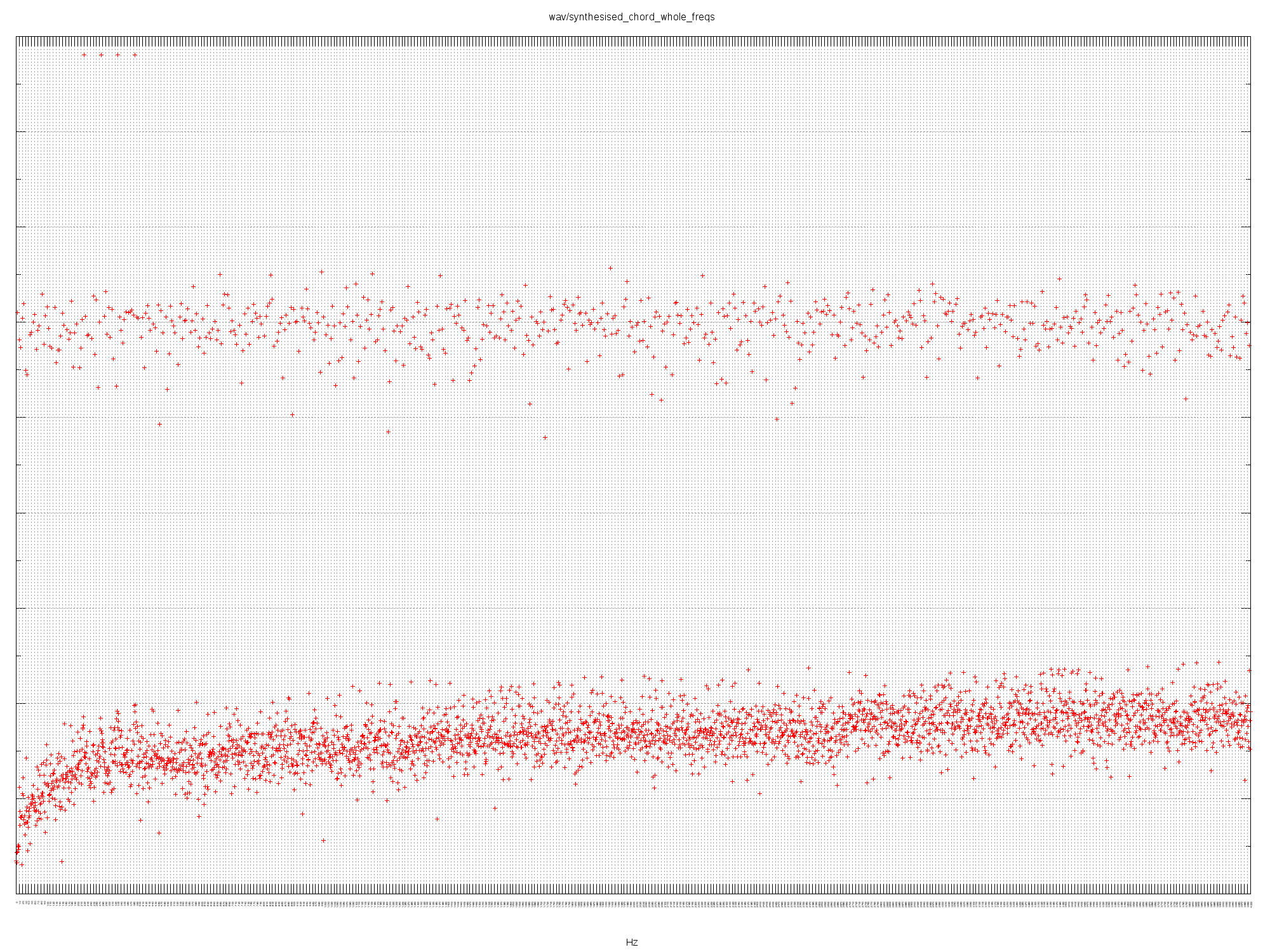 Listen to the audio.
Listen to the audio.
SYNTHESISED OVERTONES
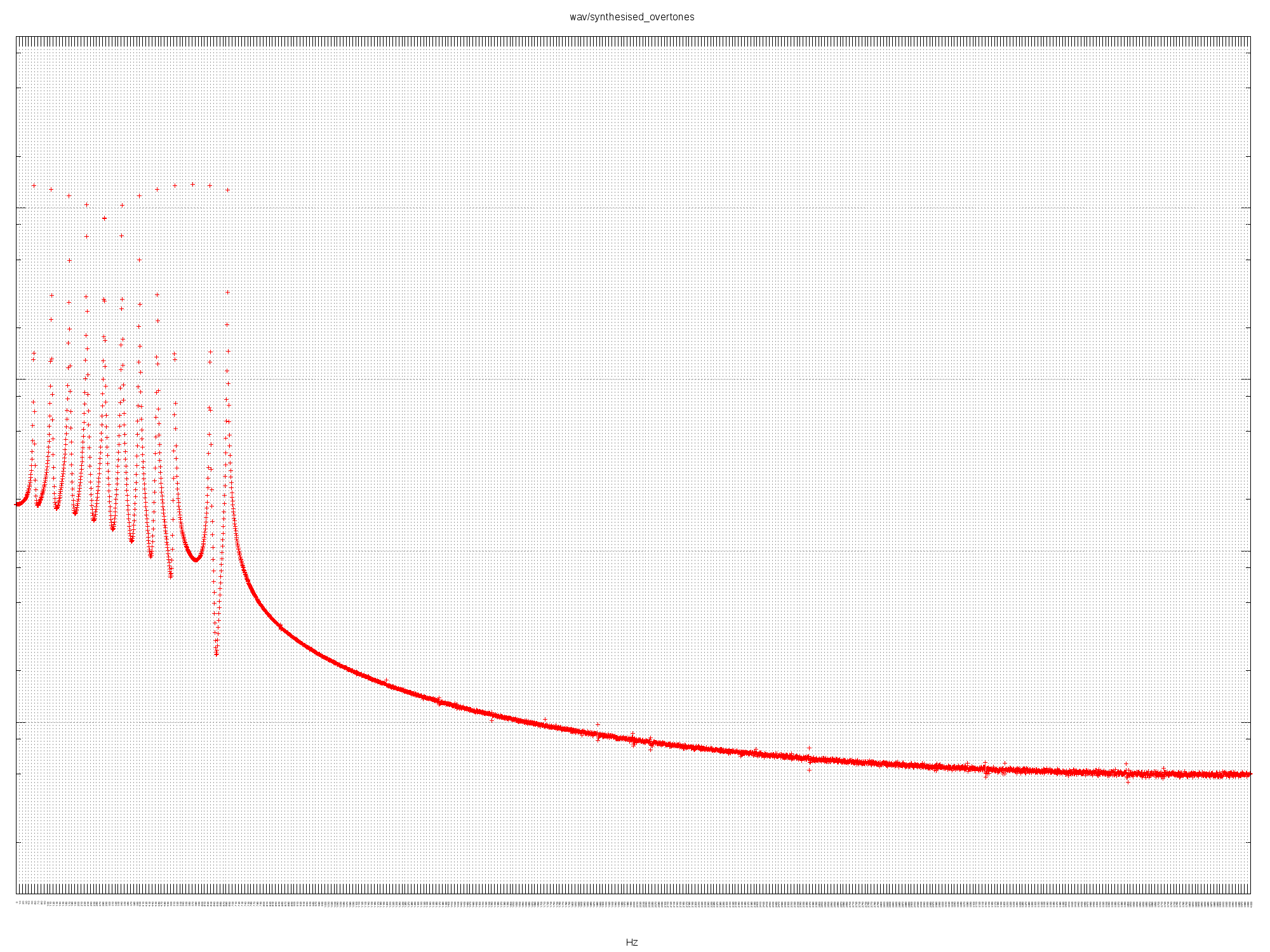 Listen to the audio.
Listen to the audio.